本文所分析的DDPM论文以及代码的相关信息如下:
一、算法流程
论文核心方法: 在扩散模型上作出两个方面的改进提升,即改进模型架构(Architecture Improvements)和使用分类器引导(Classifier Guidance),从而在FID上获得优于GAN的表现。
1.通过设计一系列的消融实验,比较各部分改进对FID的影响,最终确定使用架构如下:

2.使用分类器引导的DDPM和DDIM的算法流程分别如下:


二、 代码分析
2.1 分类引导采样流程
采样步骤包括:
- 加载UNet模型 (预测噪声$\theta$) 和扩散模型 ($\mu_\theta(x_t),\sigma_\theta(x_t)$);
- 加载预训练好的分类噪声图像的分类器 $p_\phi(y|x_t)$;
- 进行DDPM或DDIM采样过程,并加入引导梯度;
- 将样本转化为图片并保存。
相关核心函数调用见下图(以DDPM采样为例):
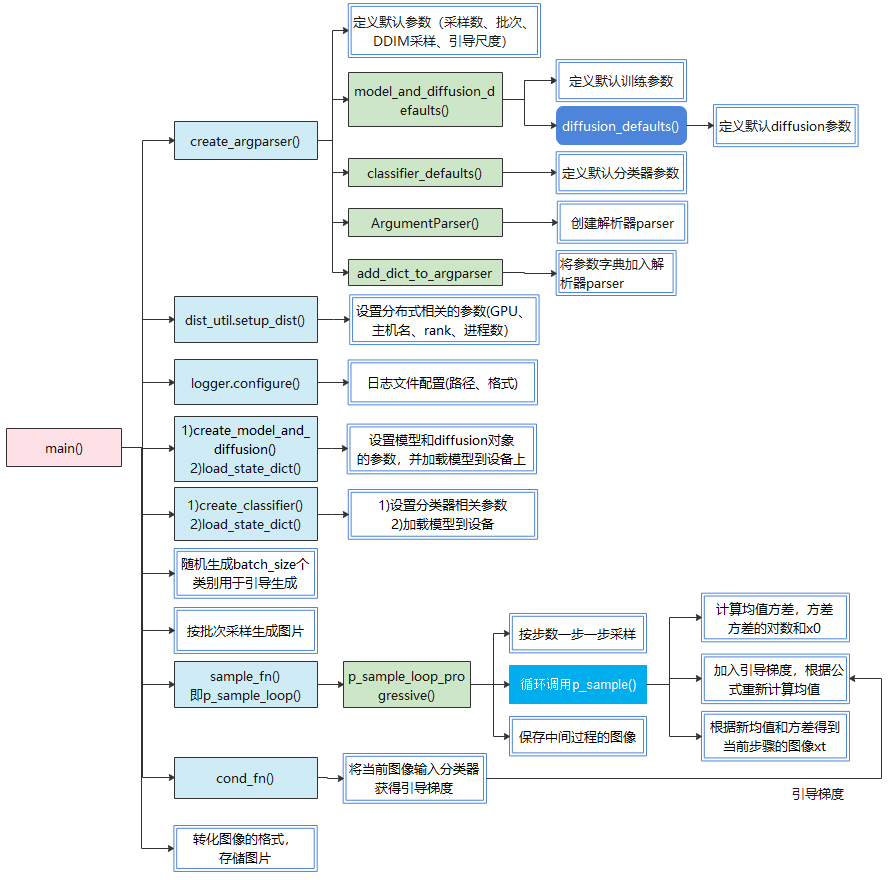
classifier_sample.py代码如下:
1#使用一个噪声图像分类器来引导采样过程,从而生成更逼真的图像
2#非核心代码已省略....
3def main():
4 logger.log("creating model and diffusion...")
5 model, diffusion = create_model_and_diffusion(#初始化UNet模型和扩散模型
6 **args_to_dict(args, model_and_diffusion_defaults().keys()))
7 model.load_state_dict(
8 dist_util.load_state_dict(args.model_path, map_location="cpu"))
9 model.to(dist_util.dev())
10 if args.use_fp16:
11 model.convert_to_fp16()#使用浮点进行原始模型的训练推理,float16加快速度
12 model.eval()#.train()模式主要用于激活某些特定于训练的层如Dropout和BatchNorm)
13 # 而.eval()模式则确保这些层在评估或测试时不激活
14 logger.log("loading classifier...")
15 classifier = create_classifier(**args_to_dict(args, classifier_defaults().keys()))
16 #.... 与加载model类似
17 logger.log("sampling...")
18 def model_fn(x, t, y=None):#预测噪声
19 assert y is not None
20 return model(x, t, y if args.class_cond else None)
21 all_images = []
22 all_labels = []
23 while len(all_images) * args.batch_size < args.num_samples:
24 model_kwargs = {}
25 classes = th.randint(
26 low=0, high=NUM_CLASSES, size=(args.batch_size,), device=dist_util.dev()
27 )#输出长度为batch_size的列表,每个元素在(0~num_classes)之间
28 model_kwargs["y"] = classes
29 #若存在,在Unet模型计算时会作为条件嵌入与时间嵌入叠加,以条件信息指导模型生成
30 sample_fn = (
31 diffusion.p_sample_loop if not args.use_ddim else diffusion.ddim_sample_loop
32 ) # 选择具体采样函数,是否使用ddim方法
33 sample = sample_fn(
34 model_fn, #预测噪声的UNet模型
35 (args.batch_size, 3, args.image_size, args.image_size),
36 # 此为采样时图像的尺寸[batch_size, 3, image_size, image_size]
37 clip_denoised=args.clip_denoised,
38 model_kwargs=model_kwargs,
39 cond_fn=cond_fn, #分类器引导
40 device=dist_util.dev(),
41 )
42 # 将图片每个位置的数值转为0~255区间内,即还原为图片
43 sample = ((sample + 1) * 127.5).clamp(0, 255).to(th.uint8)
44 sample = sample.permute(0, 2, 3, 1) # [batch_size, image_size, image_size, 3]
45 sample = sample.contiguous()
46
47 # 将多卡中的采样的样本图片和推定的label集合
48 gathered_samples = [th.zeros_like(sample) for _ in range(dist.get_world_size())]
49 dist.all_gather(gathered_samples, sample) # gather not supported with NCCL
50 all_images.extend([sample.cpu().numpy() for sample in gathered_samples])
51 gathered_labels = [th.zeros_like(classes) for _ in range(dist.get_world_size())]
52 dist.all_gather(gathered_labels, classes)
53 all_labels.extend([labels.cpu().numpy() for labels in gathered_labels])
54 logger.log(f"created {len(all_images) * args.batch_size} samples")
55
56 arr = np.concatenate(all_images, axis=0)
57 arr = arr[: args.num_samples]
58 label_arr = np.concatenate(all_labels, axis=0)
59 label_arr = label_arr[: args.num_samples]
60 if dist.get_rank() == 0:
61 shape_str = "x".join([str(x) for x in arr.shape])# 10x64x64x3
62 out_path = os.path.join(logger.get_dir(), f"samples_{shape_str}.npz")
63 logger.log(f"saving to {out_path}")
64 np.savez(out_path, arr, label_arr)
65 dist.barrier()
66 logger.log("sampling complete")
67#......初始化所需参数
68if __name__ == "__main__":
69 main()
其中,关键函数cond_fn用于生成引导梯度:
1def cond_fn(x, t, y=None):#核心函数,返回分类器引导梯度
2 assert y is not None
3 with th.enable_grad():
4 x_in = x.detach().requires_grad_(True)
5 logits = classifier(x_in, t)
6 log_probs = F.log_softmax(logits, dim=-1)
7 selected = log_probs[range(len(logits)), y.view(-1)]
8 return th.autograd.grad(selected.sum(), x_in)[0] * args.classifier_scale
这里的t是当前时间步,x是当前步的去噪结果图,y是类别索引。计算分类梯度的过程如下:
- 首先把
x和原始的梯度断开(detach),准备计算分类器的梯度; - 把
x_in和t都输入到分类器中,得到分类器预测的类别logits:- 分类带噪声图像,输入图像$x_t$的同时也要输入当前时间步t,告知分类器当前噪声的强度;
- 故在分类引导中,不用重新训练 diffusion 模型,但要单独训练一个噪声图像分类器。
- 再把预测的类别
logits过一下softmax,得到各类别的概率log_probs; - 从
log_probs中取出我们指定的类别y对应的概率,即selected; - 最后将
selected中各个目标类别的概率值加在一起(因为一次要处理batch_size张图片),希望该值越大越好,取该值对于x的梯度,即为分类器引导的梯度。
2.2 gaussian_diffusion.py——采样过程代码
(1)采用DDPM采样方法时,sample_fn()即p_sample_loop(),该方法通过p_sample_loop_progressive()来循环调用p_sample一步步采样,p_sample进行$p(x_{t-1}|x_t,y)$采样,过程步骤如下:
- 得到模型预测的噪声 $\epsilon_\theta(x_t,t,y)$,再计算出均值 $\mu_\theta(x_t)$和方差 $\Sigma(x_t)$;
- 加上条件引导,得到新的均值 $\mu=\mu_\theta(x_t)+s\Sigma(x_t)\nabla\log p_\phi(y|x_t)$;
- 重参数技巧,从高斯分布中采样z,再得到
sample:$x_{t-1}=\mu+\Sigma z$.
1def p_sample(
2 self,
3 model,
4 x,
5 t,
6 clip_denoised=True,
7 denoised_fn=None,
8 cond_fn=None,
9 model_kwargs=None,):
10 out = self.p_mean_variance( #通过模型预测的噪声计算均值与方差
11 model,
12 x,
13 t,
14 clip_denoised=clip_denoised,
15 denoised_fn=denoised_fn,
16 model_kwargs=model_kwargs,)
17 noise = th.randn_like(x)#从高斯分布中采样z
18 nonzero_mask = (
19 (t != 0).float().view(-1, *([1] * (len(x.shape) - 1)))
20 ) # no noise when t == 0
21 if cond_fn is not None:
22 out["mean"] = self.condition_mean(#计算加入引导的新均值
23 cond_fn, out, x, t, model_kwargs=model_kwargs)
24 #重参数采样技巧
25 sample = out["mean"] + nonzero_mask * th.exp(0.5 * out["log_variance"]) * noise
26 return {"sample": sample, "pred_xstart": out["pred_xstart"]}
调用condition_mean来计算加入引导后的均值:
1def condition_mean(self, cond_fn, p_mean_var, x, t, model_kwargs=None):
2 gradient = cond_fn(x, self._scale_timesteps(t), **model_kwargs)
3 new_mean = (
4 p_mean_var["mean"].float() + p_mean_var["variance"] * gradient.float()
5 )#重新计算均值
6 return new_mean
(2)采用DDIM采样方法
sample_fn()即ddim_sample_loop,该方法通过ddim_sample_loop_progressive来循环调用ddim_sample进行采样,p_sample方法实现 $p(x_{t-1}|x_t,x_0,y)$ 过程,采样步骤如下:
- 得到模型预测的噪声 $\epsilon_\theta(x_t)$;
- 加入梯度引导后得到新的噪声 $\hat{\epsilon}=\epsilon_\theta(x_t)-\sqrt{1-\alpha_t}\nabla\log p_\phi(y|x_t)$;
- 得到新的预测的 $\hat{x_0}=\frac{(x_t-\sqrt{ 1-\alpha_t}\hat{\epsilon})}{\sqrt{\alpha_t}}$;
- 再由论文中的公式(12)得: $x_{t-1}= \sqrt{\alpha_{t-1}}x_0+\sqrt{1-\alpha_{t-1}-\sigma_t^2}\epsilon_\theta(x_t)+\sigma_t\epsilon_t$,在DDIM中,有$\sigma=0$,故公式化简为 $x_{t-1}= \sqrt{\alpha_{t-1}}\hat{x_0}+\sqrt{1-\alpha_{t-1}}\epsilon_\theta(x_t)$.
代码如下:
1def ddim_sample(
2 self,
3 model,
4 x,
5 t,
6 clip_denoised=True,
7 denoised_fn=None,
8 cond_fn=None,
9 model_kwargs=None,
10 eta=0.0,):
11 out = self.p_mean_variance(
12 model,
13 x,
14 t,
15 clip_denoised=clip_denoised,
16 denoised_fn=denoised_fn,
17 model_kwargs=model_kwargs,)
18 if cond_fn is not None:
19 out = self.condition_score(cond_fn, out, x, t, model_kwargs=model_kwargs)
20 eps = self._predict_eps_from_xstart(x, t, out["pred_xstart"])#预测的噪声与x0可以互相转化
21 alpha_bar = _extract_into_tensor(self.alphas_cumprod, t, x.shape)
22 alpha_bar_prev = _extract_into_tensor(self.alphas_cumprod_prev, t, x.shape)
23 #eta=0.0,sigma实际在DDIM中为0
24 sigma = (eta * th.sqrt((1 - alpha_bar_prev) / (1 - alpha_bar))
25 * th.sqrt(1 - alpha_bar / alpha_bar_prev))
26 # Equation 12.
27 noise = th.randn_like(x)
28 mean_pred = (
29 out["pred_xstart"] * th.sqrt(alpha_bar_prev)
30 + th.sqrt(1 - alpha_bar_prev - sigma ** 2) * eps
31 )
32 nonzero_mask = (
33 (t != 0).float().view(-1, *([1] * (len(x.shape) - 1)))
34 ) # no noise when t == 0
35 sample = mean_pred + nonzero_mask * sigma * noise
36 return {"sample": sample, "pred_xstart": out["pred_xstart"]}
调用condition_score来计算加入引导后的噪声与与预测图像 $x_0$:
1def condition_score(self, cond_fn, p_mean_var, x, t, model_kwargs=None):
2 alpha_bar = _extract_into_tensor(self.alphas_cumprod, t, x.shape)
3 eps = self._predict_eps_from_xstart(x, t, p_mean_var["pred_xstart"])
4 eps = eps - (1 - alpha_bar).sqrt() * cond_fn(
5 x, self._scale_timesteps(t), **model_kwargs)#加入引导梯度后的噪声
6 out = p_mean_var.copy()
7 out["pred_xstart"] = self._predict_xstart_from_eps(x, t, eps)#重新计算x0
8 out["mean"], _, _ = self.q_posterior_mean_variance(
9 x_start=out["pred_xstart"], x_t=x, t=t
10 )
11 return out