一、论文简介

DENOISING DIFFUSION IMPLICIT MODELS

会议来源：ICLR   文章年限：2021

核心思路：在DDPM(DENOISING DIFFUSION probabilistic MODEL)的启发下，用非马尔可夫过程改变生成过程，不用一步一步去噪，从而能够更快地产生高质量样本。

二、论文理解

1. 背景与目的

  已经有多种模型都在图片生成上展示出了或多或少的优势。其中GAN比基于似然的模型如变分自动编码器、自回归模型表现出更高的样本质量。但是同时，GAN也具有一些不可忽视的缺点：训练过程不稳定；在某些情况下，GAN可能会遇到模式崩溃，导致生成的样本质量下降。

  针对这一不足，基于马尔可夫链的迭代生成模型应运而生，如DDPM和噪声条件评分模型，它们不需要对抗训练，也同样可以生成较好质量的样本。但是同样也存在一个关键的缺点——迭代次数多，生成样本的速度慢。

  为了提高采样速度，在DDPM的启发下，在损失目标函数相同的情况下，作出了相应的改进，提出了DDIM。DDIM相较于DDPM的优点：

  • 在保证提高10到50倍的采样速度的同时，有更高的生成质量
  • 有一致性属性——在初始潜在变量相似的情况下，由不同长度的马尔可夫链生成的样本具有相似的高层特征。
  • 利用“一致性”，可以通过初始潜在变量来进行在语义上有意义的图像插值

2. 核心方法

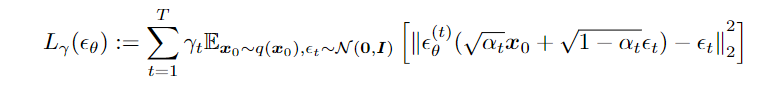  以生成过程为切入点，一个关键的观察结果是，Lγ 形式的 DDPM 目标仅取决于边际值q(xt|x0)，而不直接取决于联合 q(x1:T |x0)。由此得到启发：DDPM这个隐变量模型可以有很多推理分布来选择，只要推理分布满足边缘分布条件（扩散过程的特性）即可，而且这些推理过程并不一定要是马尔卡夫链。   由于有许多具有相同边际的推理分布，因此可以找出非马尔可夫的替代推理过程，从而产生新的生成过程（图 1，右）。这些非马尔可夫推理过程产生与 DDPM 相同的代理目标函数。

2.1 非马尔可夫链的前向过程

  推理分布族 Q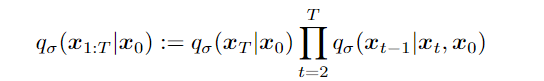： 其中 $q_\sigma(x_T|x_0) = \mathcal{N}(\sqrt{\alpha_T}x_0,(1-\alpha_T)I)$ 且 $t>1$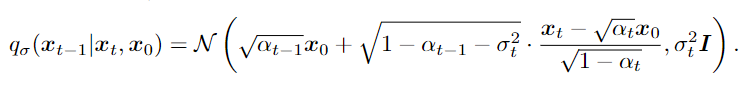，   由贝叶斯公式可以得出：

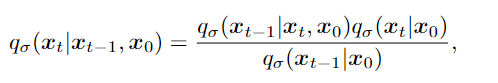
  这里每个 xt 都可以依赖于 xt−1 和 x0，因此前向过程不再是马尔可夫的。 当 σ → 0 时，达到了一种极端情况，只要在某个 t 内观察 x0 和 xt，那么 xt−1 就已知并固定。（！！！公式代入推理）

2.2 生成过程和统一变分推理目标

  （1）生成过程pθ (x0:T )：每一步的去噪都是从过程qσ(xt−1|xt, x0)中学习，σ 的大小控制着前向过程的随机性；

先由给定的xt 预测出x0(见公式9) 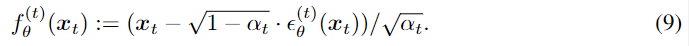然后得到生成过程

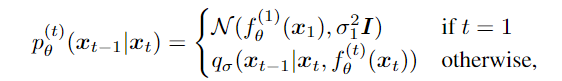
通过样本 xt 生成样本 xt−1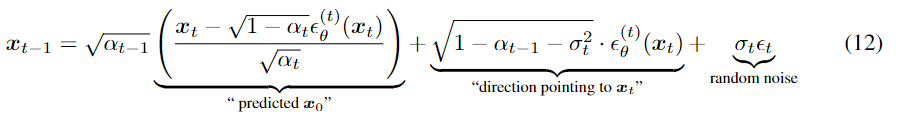： 通过改变σ 的可以改变生成过程，当$σ_t = \sqrt{(1 − α_{t−1})/(1 − α_t)}\sqrt{1 − α_t/α_{t−1}}$时，就是马尔可夫链的DDPM。（！！！公式推理）

当$σ_t = 0$ 时，即随机噪声t之前的系数变为零，则样本是通过固定过程（从 xT 到 x0）从潜在变量生成的。（！！！公式推理）

  （2）噪声预测中θ的优化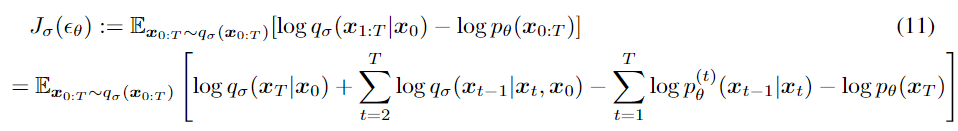： 变形基于如下公式：

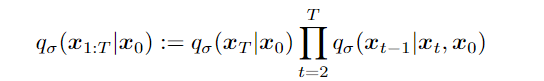
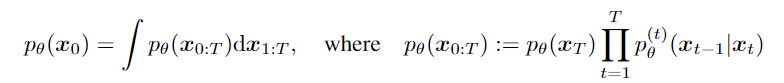
  （3）目标函数的等价：

对于所有 σ > 0，存在 γ ε RT >0 且 C ε R，使得 Jσ = Lγ + C

  作者指出：变分目标 Lγ 的特殊之处在于，如果模型 (t) 的参数 θ 不在不同 t之间共享，则 θ 的最优解将不依赖于权重 γ(γ := [γ1, . 。 。 , γT ] 是目标中取决于 α1:T 的正系数向量)。Lγ 的这一性质有两个含义。一方面，这证明了使用 L1 作为 DDPM 变分下界的替代目标函数是合理的；另一方面，由于Jσ与定理1中的某个Lγ等价，因此Jσ的最优解也与L1的最优解相同。因此，如果模型 θ 中的参数不跨 t 共享，则在DDPM中使用的 L1 也可以用作变分目标 Jσ 的替代目标函数。

  另外，有提到与 NEURAL ODES的联系。查阅了解到，Neural ODE（Neural Ordinary Differential Equations，神经常微分方程）是一种基于常微分方程的深度学习方法，它结合了传统的ODE数值求解技术和神经网络模型。

PS：τ用于控制获取样本的速度； σ用于在确定性 DDIM 和随机 DDPM 之间插值。

三、优点及支撑

  主要与DDPM相比：

  1. 质量与效率——当考虑较少的迭代时，DDIM 在图像生成方面优于 DDPM，与原始 DDPM 生成过程相比，速度提高了 10 倍到 100 倍。

  下表展示了在数据集CIFAR10 和 CelebA 上，改变用于生成样本的时间步数 (dim(τ )) 和过程的随机性 (η)，得到的图像的质量。（实际是在图像质量与计算成本之间trade-off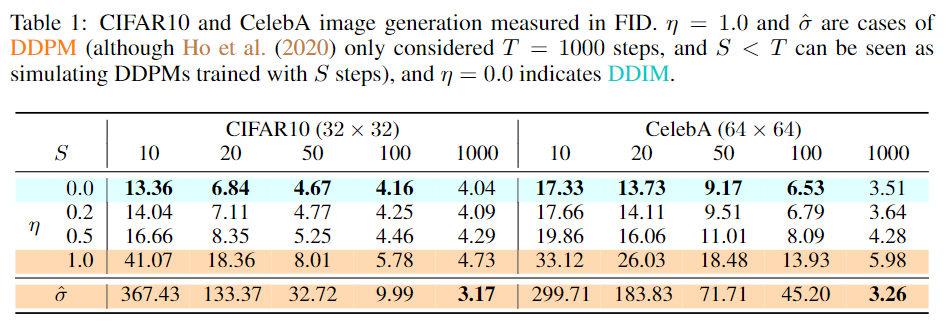）：   可以看到当时间步长较小时，DDIM (η = 0) 实现了最佳样本质量，而在具有相同时间步长时，DDPM (η = 1 和 ˆσ) 与随机性较小的对应样本相比，表现较差。从上表也可以看到在 CelebA 上，100 步 DDPM 的 FID 分数与 20 步 DDIM 相似。

  下图也证明了随机性越大，图片质量越差。

  DDIM 能够在 20 到 100 个步骤内生成质量与 1000 个步骤模型相当的样本，与原始 DDPM 相比，速度提高了 10 到 50 倍。

  1. 具有“一致性”属性——一旦初始潜在变量 xT 固定，无论生成轨迹如何，DDIM 都会保留高级图像特征，因此它们能够直接从潜在空间执行插值。   在许多情况下，仅 20 步骤生成的样本在高级特征方面就已经与 1000 步骤生成的样本非常相似，只有细节上的微小差异。合理推论： xT是图像的信息性潜在编码，而参数是影响图像质量的细节性编码。   上图表明 xT 中的简单插值可以在两个样本之间产生语义上有意义的插值

  2. 低的重建误差——对样本进行编码，然后从潜在编码中重建样本，而 DDPM 由于随机采样过程而无法做到这一点，与OEDs部分相关。 可以看到DDIM 具有较低的重建误差，并且具有类似于神经常微分方程和归一化流的属性。

PS：FID用于衡量两组图像的相似度，是计算真实图像和生成图像的特征向量之间距离的一种度量。FID 在最佳情况下的得分为 0.0，表示两组图像相同。分数越低代表两组图像越相似，或者说二者的统计量越相似。

四、未来工作与不足

  未来工作：

  1. 原则上，根据DDIM，可以训练具有任意数量的前向步骤的模型，而仅在生成过程中从其中的一些步骤中进行采样。因此，训练后的模型可以允许更多的扩散步骤。这方面的实证研究留作未来的工作。

  2. 由于 DDIM 的采样过程与神经 ODE 的采样过程类似，因此看看是否有减少 ODE 中离散化误差的方法。

  3. 研究 DDIM 是否表现出现有隐式模型的其他属性。

  不足：在小图像的数据集上表现很好，但在大图像上呢？